Euclid’s proof of the infinitude of primes is justly famous. Here is one version of this proof:
Let P be a finite set of primes, and let N be the product of the numbers in P. Then N+1 is not divisible by any number in P, since it leaves a remainder of 1. But N+1 must be divisible by at least one prime, so P cannot contain all of the primes. Therefore the set of primes is infinite.
A variation of this argument shows that there are infinitely many primes of the form  .
.
Let P be a finite set of primes of the form  , and let N be the product of the primes in P. Consider the number
, and let N be the product of the primes in P. Consider the number 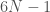 . It is not divisible by 2 or 3, nor is it divisible by any number in P. But it is not possible that all prime factors of
. It is not divisible by 2 or 3, nor is it divisible by any number in P. But it is not possible that all prime factors of 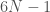 have the form
have the form  , because the product would have the form
, because the product would have the form  as well.
as well.
Therefore, 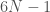 has at least one prime factor of the form
has at least one prime factor of the form  that does not belong to P. Therefore, P cannot contain every prime of the form
that does not belong to P. Therefore, P cannot contain every prime of the form  , so the set of primes of this form is infinite.
, so the set of primes of this form is infinite.
It takes a little bit more work to prove that there are infinitely many primes of the form  . Here is a proof of that fact.
. Here is a proof of that fact.
Let P be a finite set of primes of the form  , and let N be a number that is divisible by every number in P. Assume that N is also divisible by 6. Let p be a prime divisor of
, and let N be a number that is divisible by every number in P. Assume that N is also divisible by 6. Let p be a prime divisor of  .
.
Note that 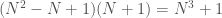 . so p divides
. so p divides 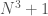 , or in other words
, or in other words 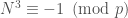 and so
and so  .
.
Recall that the order of N modulo p is the least positive k so that  . The order must divide 6. so k = 1, 2, 3, or 6. But
. The order must divide 6. so k = 1, 2, 3, or 6. But 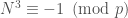 , so the order cannot be 1 or 3.
, so the order cannot be 1 or 3.
Can the order be 2? If  and
and 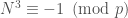 then
then  . This would be bad, because then p would divide both
. This would be bad, because then p would divide both  and
and  ; but
; but 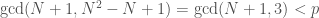 , contradiction.
, contradiction.
Thus N has order 6 mod p, and the group of units mod p has order 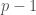 , so 6 divides
, so 6 divides 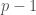 , which means that p has the form
, which means that p has the form  . Therefore, P does not contain all primes of the form
. Therefore, P does not contain all primes of the form  , so the set of primes of this form is infinite.
, so the set of primes of this form is infinite.
and
. After substituting,
. Therefore
, so there are no whole number solutions.
