The Pyramids of Mars
The other day, I was having a nice conversation with a young exchange student from Mars. He explained to me that mathematics is very different on his planet, because they use triangles instead of squares.
“What on Earth do you mean?” I replied.
He took out a pad of paper and drew a square array of 25 dots, arranged in 5 rows and 5 columns.
“Yes, of course,” I said, somewhat impatiently. “Your picture clearly shows that 5 squared is 25. Are you telling me that it’s different on Mars?”
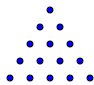
My Martian friend was unperturbed. “Certainly, 5 squared is 25 on Mars, and everywhere else in the universe. But we prefer triangles to squares. Can you guess what “5 triangled” means?
“Well, I think that 5 triangled must be 15, since 1+2+3+4+5 = 15.” I drew a picture like this.
“That is correct. On my planet, we write 52 = 15. An exponent of 2 means triangled instead of squared.”
I pondered this for a moment. “OK, if the second power is a triangle, what is the third power? Is it a pyramid?”

Pyramid of 35 spheres
“That’s the idea. It’s a tetrahedron, to be precise. In Martian mathematics, a third power is the sum of consecutive triangular numbers. For example, 53 = 1 + 3 + 6 + 10 + 15 = 35.”
This made sense to me, but I still had a nagging doubt. “We can only see objects in three dimensions. Are higher powers possible in Martian mathematics?
“Yes, of course. The pattern continues forever, even if we can’t draw the pictures. A fourth power is a sum of consecutive third powers, a fifth power is a sum of consecutive fourth powers, and so on.”
It was starting to make sense. “Does that mean that 54 = 1 + 4 + 10 + 20 + 35 = 70 in Martin mathematics?”
My friend confessed that he wasn’t sure. Fourth powers had always given him trouble in school. But he pulled out a Martian calculator (shaped like a triangle, of course) and confirmed that my calculation was correct.
Naturally, I had a million other questions about Martian mathematics. Do they have triangular roots instead of square roots? Does the quadratic formula become a triangle-atic formula? Is there a Martian equivalent of the binomial theorem? But my friend was tired, and he suggested that I should ask his old Martian professor instead. I have arranged a meeting with her, and I will let you know what I learn.